MOL ECULAR PR OPERTIES O PTIMIZATION PROJECT

Thermodynamic 3D  Description of  H-bonding.

Most modern procedures for three-dimensional (3D) computer-assisted drug design use force-field calculations to take H-bonding into account. These calculations are used in many research areas including conformational analysis, pharmacophore identification, ligand docking, de novo ligand design, comparative molecular field analysis (CoMFA), and the identification of favorable binding sites from molecular interaction fields .

On the basis of a sophisticated and  parameterized method called GRID, Goodford et al. [1-3] made efforts to improve the calculation of the H-bond contribution to the interaction energy of ligand-macromolecular complexes. The GRID method is parameterized by fitting experimental X-ray data from protein and small-molecule crystals, and is designed to calculate the interactions of a probe (a small molecule such as water or ammonia) and a macromolecular system. An 8-6 function was adopted, and was found to give satisfactory result [2]:

E_r = C/r⁸ - D/r⁶     (1),

where C = -3E_mr⁸A⁸/mol; D = -4E_mr_m⁶A⁶/mol ; r is the distance between the acceptor atom and the donor heavy atom; E_m is optimum H-bond enthalpy in kcal/mole; r_m is the optimum H-bond length.

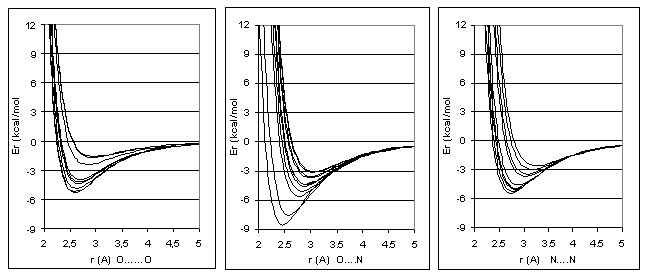
However there are only three fixed optimum H-bond lengths in the GRID framework: 2.8 A for “O…O”, 3.0 A for “N…O” and 3.2 A for “N…N” . And the wide intervals of enthalpy values for each those type of H-bond complexes (see previous Chapter)  permit to suppose any dependence between energies and distances even in the case of optimum arrangement of atoms participating in H-bonding. Hence, to create a realistic platform for the quantitative 3D description of H-bonding, one must recognize that optimum H-bond energies (E_m) depend on optimum H-bond distances (r_m) for the different types of H-bonds in complex formation. This our study is presented in [4].

First of all  we selected from Cambridge Structural Database 58 "ideal" H-bond complexes where the angles of the donor heavy atom, hydrogen and acceptor atoms were in the range of 173° to 187° and angles of the acceptor nucleus, the lone pair of electrons and the hydrogen atom were in the range of 170° to 190°. There were 13 such “O-H…O” complexes, 19 ”O-H…N” or “N‑H…O” complexes, and 26 “N-H…N” complexes among the 58 "ideal" representatives.

Because there are significant differences between the covalent and van der Waals radii of oxygen and nitrogen atoms, we decided to look for relationships between optimum energy (E_m) and optimum distances (r_m) in those three subsets. Such relationships are not expected to be linear because energy values approach zero as distances increase. In this study we used a sigmoid function:

E_m = k₄/(1 + 10^k₅^+k₆^rm)    (2)

Values of k₄ in eq. (2) may be fixed, and are limited by the maximum values for the enthalpies. Rearranging eq. (2) and simplifying the constants gives eq. (3):

r_m = k₇log[(k₄-E_m)/(E_m)] + k₈      (3)

Using eq. (3), we can now calculate r_m from E_m values. Thus, for each specific pair of atoms participating in an H-bond, its H-bonding potential can be calculated. The potentials fot 58 “ideal” complexes are presented on the fig.:

Hence, a scheme to calculate the H-bonding energies of atoms in a three-dimension arrangement can be carried out by following steps:

1. Use HYBOT’s acceptor and donor enthalpy factors to estimate the optimum H-bonding energy.

2. Estimate the optimum H-bonding distance corresponding to the calculated energy optimum by means of eq. (3) .

3. Use eq. (1) or other functions to take into account the distance and angle deviations of the atoms involved.

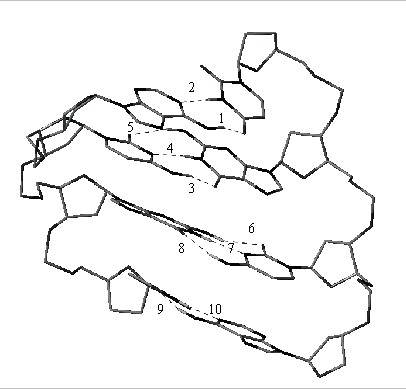
An example of such calculation for a model system is presented in [4]. This represents the interactions of bases in double helix of RNA in A form.

These calculations were carried out by means of 3D HYBOT in UNIX, a new program, by considering only H-bonding interactions and Sybyl . We believe it is possible that this approach to H-bond calculations will not be too difficult to integrate with existing and future force-field schemes to produce a superior method to estimate intermolecular interactions in any three dimensional framework.

3-D hydrogen bond descriptors.

References:

1.     Goodford, P.J., J.Med.Chem., 28 (1985) 849.

2.     Wade, R.C., Clark, K. and Goodford, P.J., J.Med.Chem., 36 (1993) 140,148.

3.      Goodford, P.J., J.Chemometrics, 10 (1996) 107.

4.     Raevsky O.A. and Skvortsov, V.S., 3D Hydrogen Bond Thermodynamics (HYBOT) Potentials in Molecular Modelling, Comp.-Aided Mol.Des., 16, 1 (2002).